204x Filetype PDF File size 0.26 MB Source: unh.edu
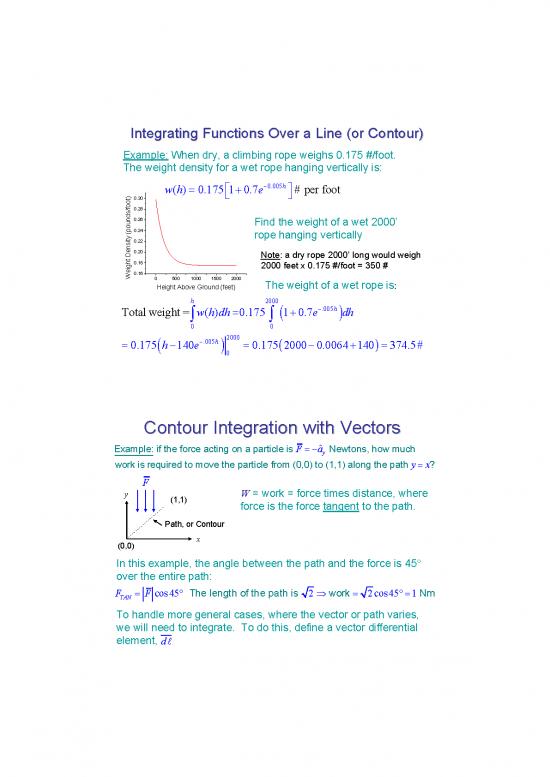
Integrating Functions Over a Line (or Contour)
Integrating Functions Over a Line (or Contour)
Example: When dry, a climbing rope weighs 0.175 #/foot.
The weight density for a wet rope hanging vertically is:
−0.005h
wh()=+0.175 1 0.7e # per foot
)0.30
/foot0.28
nds0.26 Find the weight of a wet 2000’
pou0.24
( rope hanging vertically
ity0.22
ens0.20 Note: a dry rope 2000’ long would weigh
0.18 2000 feet x 0.175 #/foot = 350 #
Weight D0.16
0 500 1000 1500 2000 The weight of a wet rope is:
Height Above Ground (feet)
h 2000
−.005h
Total weight = wh( )dh=+0.175 1 0.7e dh
()
∫∫
00
−.005h 2000
=−0.175 he140 =0.175 2000−0.0064+140 =374.5#
()
()
0
Contour Integration with Vectors
Contour Integration with Vectors
ˆ
Fa=−
Example: if the force acting on a particle is y Newtons, how much
work is required to move the particle from (0,0) to (1,1) along the path yx= ?
F
y (1,1) W= work = force times distance, where
force is the force tangent to the path.
Path, or Contour
(0,0) x
In this example, the angle between the path and the force is 45°
over the entire path:
FF=°cos45 The length of the path is 2 ⇒work =2cos45°=1 Nm
TAN
To handle more general cases, where the vector or path varies,
we will need to integrate. To do this, define a vector differential
element, dl
1
Differential Length Vector
Differential Length Vector
dl is an infintesimally-short vector tangent to a curve or line
dl In general, for Cartesian coordinates
dl ˆˆˆ
ddl =+xadya+dza
x yz
This can be put in terms of dx, dy, or dz only to facilitate
integration. The length of the differential length vector is:
222
dll==d ()dx +(dy)+(dz)
Vector Contour Integration
Vector Contour Integration
Needed to sum the tangential component of a
vector function along a path. Generally of the form:
Fd⋅⋅AA or Fd
v
∫∫
C
Where the second form is for a closed contour. Note
that any closed contour necessarily defines a surface.
The dot product provides a scalar representing the
component of the vector in the direction of the contour.
Example
ˆˆ
If 2 find the work required to
Fa=− +a
xy
go from (0,0) to (2,6) along the line yx=3
2
Vector Contour Integral Example
Vector Contour Integral Example
Work = F dl F = Tangential Force
∫ T T
C
dW =⋅F dll=F cosθ d
ˆˆ ˆ ˆ ˆ
F⋅=dl −22a +a ⋅dxa +dya +dza =−dx+dy
( ) ( )
xy x y z
since y = 3x on the contour, dy =3 ⇒ dy=3dx y
dx (2,6)
F⋅=ddl −23x+dx=dx
(could have put in terms of dy also) so :
2,6 y = 3x
() 2
Work = Fd⋅=l dx =2
∫∫
0,0 0
() x
(0,0)
Vector Contour Integral Example #2
Vector Contour Integral Example #2
A particle is attracted towards the origin with a force
equal to kr, where r is the distance to the origin. How
much work is required to move that particle from (0,1)
2
to (1,2) along the path y = x + 1.
y
(1,2)
Solution
(x,y)
First- find the force vector. (0,1)
2
F y = x + 1
ˆ + ˆ
Since xax yay points fromthe
origin to thepoint (x,y), then x
xˆ − ˆ
- ax yay points from(x,y) to the
origin.
3
Vector Contour Integral Example #2 (2)
(2)
Vector Contour Integral Example #2
2 2
The length of this vector is xy+=r, so
ˆˆ
F =−k()xa −ya
xy
(1,2)
ˆˆˆˆ
Work = Fd⋅⋅ll and Fd=k()−xa−ya ⋅(dxa+dya)
∫ x yxy
(0,1)
(1,2)
=−kx()dx−ydy⇒Work = k()−xdx−ydy
∫
(0,1)
12
=−kxdx−ydy=−k0.5+1.5 =−2k
()
∫∫
01
Open and Closed Contours
Open and Closed Contours
If a contour does not enclose a surface, it is an open contour:
y Example: y = x2
x
If a contour does enclose a surface, it is a closed contour:
y 2 2
Example: (x-3) +(y-2) = 1
x
4
no reviews yet
Please Login to review.